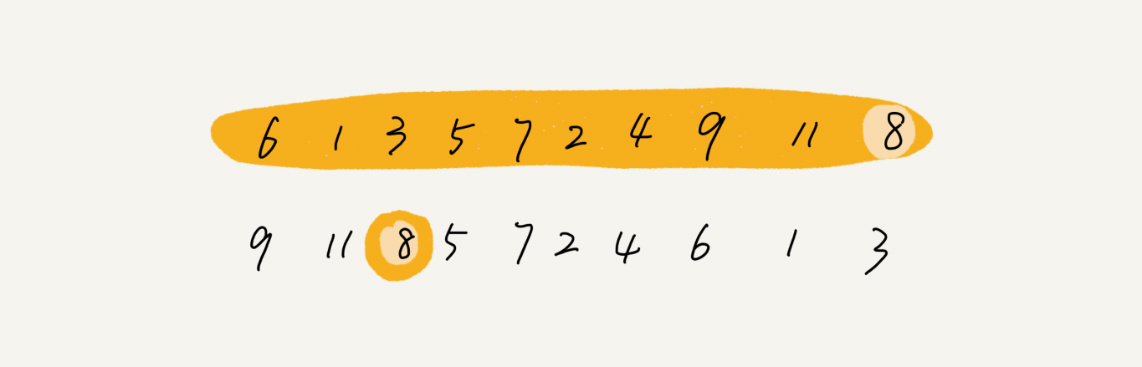上一节讲述了冒泡排序、插入排序、选择排序这三种排序算法,它们的时间复杂度都是O(n²),比较高,适合小规模数据的排序。这一节讲两种时间复杂度为O(nlogn)的排序算法,归并排序和**快速排序***。
归并排序原理
归并排序的核心思想很简单。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
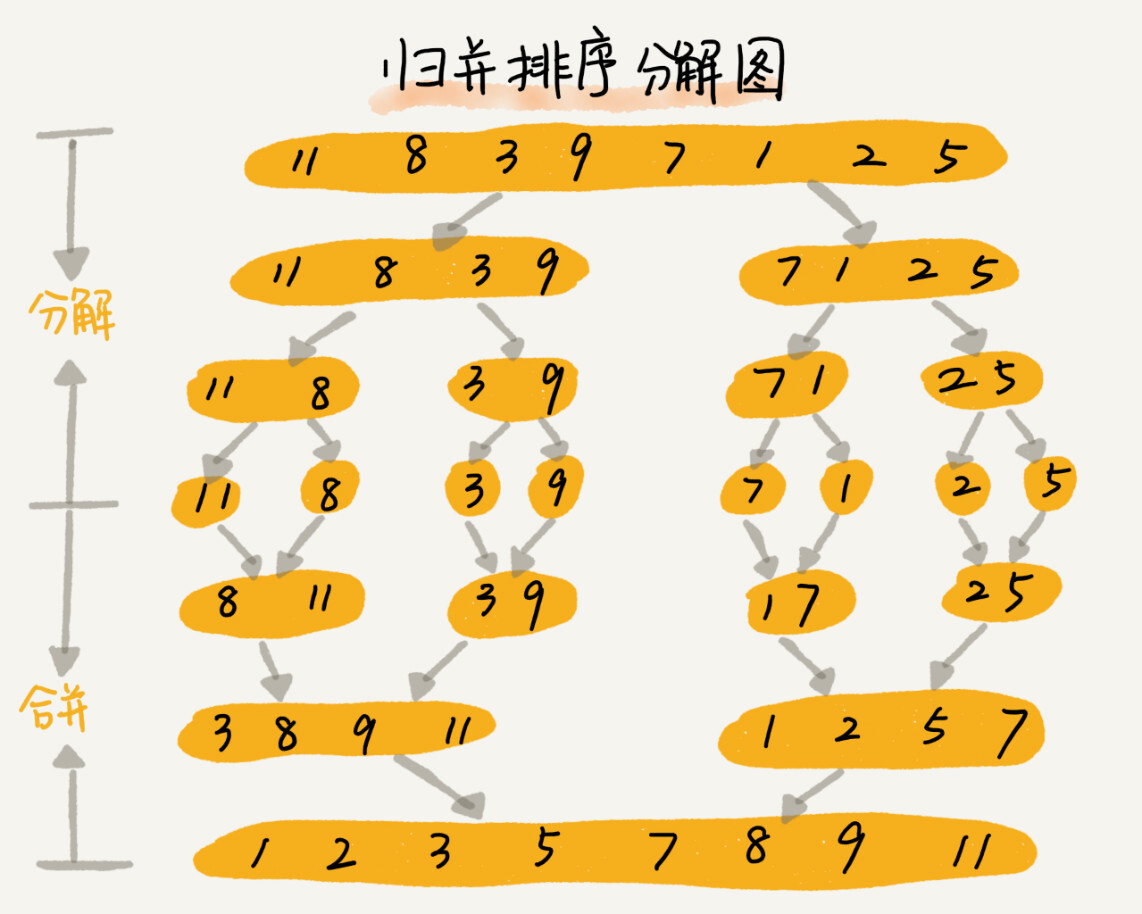
归并排序使用的是分治思想。分治,故名自已就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
分治思想跟递归思想很像。分治思想一般都是递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。
那么如何用递归代码来实现归并排序呢?
写递归代码的技巧是,分析得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。所以,要想写出归并排序的代码,我们先写出归并排序的递推公式。
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解merge_sort(p...r) 表示,给下标从p到r之间的数组排序。我们将这个排序问题转化为了两个子问题,merge_sort(p...q) 和 merge_sort(q+1...r),其中下标q等于p和r的中间位置,也就是 (p+r)/2 。当下标从p到q和从q+1到r这两个子数组都排好序之后,我们在将两个有序的子数组合并在一起,这样下标从p到r之间的数据就也排好序了。
// 归并排序算法, A是数组,n表示数组大小
merge_sort(A, n) {
merge_sort_c(A, 0, n-1)
}
// 递归调用函数
merge_sort_c(A, p, r) {
// 递归终止条件
if p >= r then return
// 取p到r之间的中间位置q
q = (p+r) / 2
// 分治递归
merge_sort_c(A, p, q)
merge_sort_c(A, q+1, r)
// 将A[p...q]和A[q+1...r]合并为A[p...r]
merge(A[p...r], A[p...q], A[q+1...r])
}你可能已经发现了,merge(A[p...r], A[p...q], A[q+1...r])这个函数的作用就是,将已经有序的 A[p...q] 和 A[q+1...r] 合并成一个有序的数组,并且放入 A[p...r]。那这个过程具体该如何做呢?
如图,我们申请一个临时数组 tmp,大小与 A[p...r] 相同。我们甩两个游标i和j,分别指向 A[p...q] 和 A[q+1...r] 的第一个元素。比较这两个元素 A[i] 和 A[j],如果 A[i]<= A[j],我们就把 A[i] 放到临时数组 tmp,并且i后移一位,否则将 A[j] 放入到数组 tmp,j后移一位。
继续上述比较过程,直到其中一个子数组中的所有数据都放入临时数组中,再把另一个数组中的数据依次加入到临时数组的末尾,这个时候,临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p...r]中。
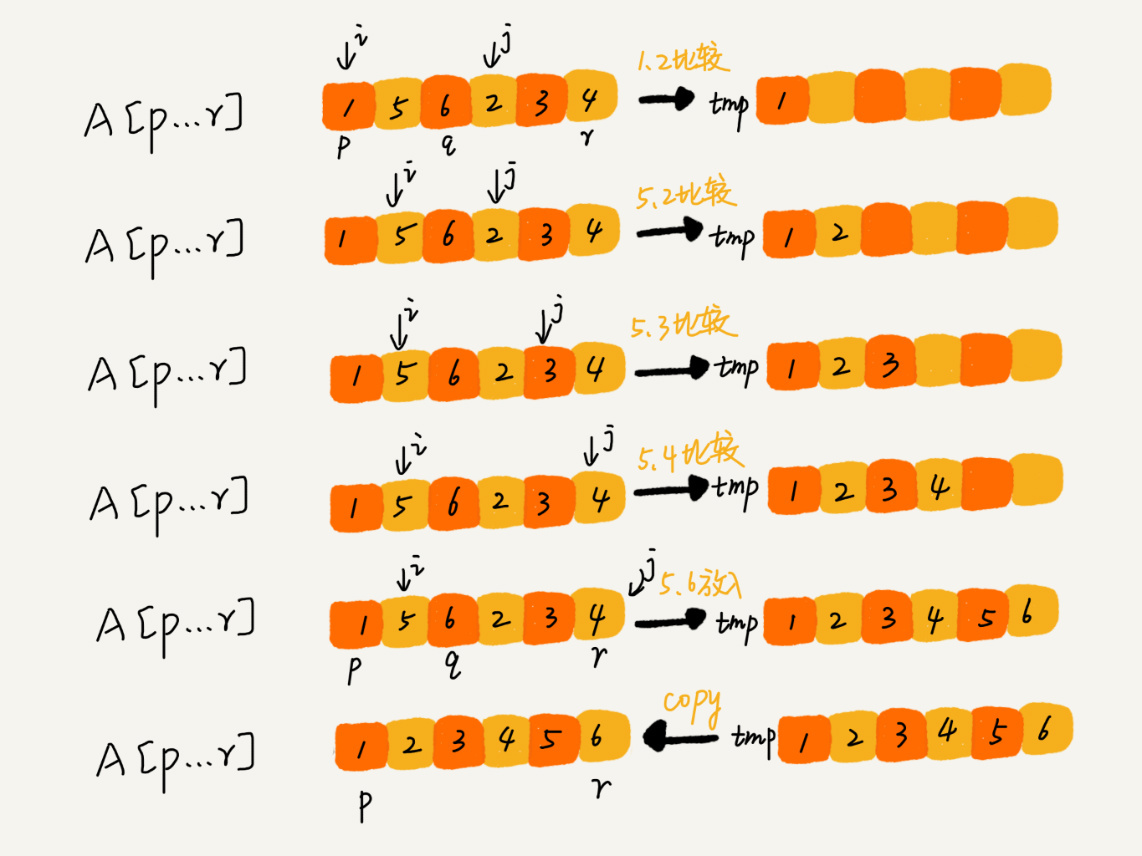
我们把 merge() 函数写成伪代码,就是下面这样:
merge(A[p...r], A[p...q], A[q+1...r]) {
var i := p,j := q+1,k := 0 // 初始化变量i, j, k
var tmp := new array[0...r-p] // 申请一个大小跟A[p...r]一样的临时数组
while i<=q AND j<=r do {
if A[i] <= A[j] {
tmp[k++] = A[i++] // i++等于i:=i+1
} else {
tmp[k++] = A[j++]
}
}
// 判断哪个子数组中有剩余的数据
var start := i,end := q
if j<=r then start := j, end:=r
// 将剩余的数据拷贝到临时数组tmp
while start <= end do {
tmp[k++] = A[start++]
}
// 将tmp中的数组拷贝回A[p...r]
for i:=0 to r-p do {
A[p+i] = tmp[i]
}
}归并排序性能
继续排序的三个问题
-
归并排序是稳定的排序算法吗?
结合前面的那张图和归并排序伪代码,你应该能发现,归并排序稳不稳定关键要看merge函数,也就是两个有序子数组合并成一个有序数组的那部分代码。
在合并的过程中,如果 A[p...q] 和 A[q+1...r] 之间有值相同的元素,那我们可以像伪代码中那样,先把 A[p...q] 中的元素放入 tmp 数组。这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。
-
归并排序的时间复杂度是多少?
归并排序设计递归,时间复杂度的分析稍微有点复杂。
递归使用的场景是,一个问题a可以分解成多个子问题b、c,那求解问题a就可以分解为求解问题b、c。问题b、c解决之后,我们再把b、c的记过合并成a的问题。
如果我们定义求解问题a的时间是 T(a),求解问题b、c的时间分别是 T(b) 和 T(c),那我们就可以得到这样的递推公式:
T(a) = T(b) + T(c) + K其中K等于将两个子问题b、c的结果合并成问题a的结果所消耗的时间。
从刚刚的分析,我们可以得到一个重要的结论:不仅递归求解的问题可以写成递推公式,递归代码的时间复杂度也可以写成递推公式。
套用这个公式,我们来分析一下归并排序的时间复杂度。
我们假设对n个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 Y(n/2)。我们知道,merge() 函数合并两个有子数组的时间复杂度是O(n)。所以,套用前面的公式,归并排序的时间复杂度计算公式就是:
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。 T(n) = 2*T(n/2) + n; n>1通过这个公式,如何来求解T(n)呢?
T(n) = 2*T(n/2) + n = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n ...... = 2^k * T(n/2^k) + k * n ......通过这样一步一步分解推倒,我们可以得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1)时,也就是 n/2^k=1,我们得到 k=log2n。我们将k值代入上面的公式,得到 T(n)=Cn+nlog2n。如果我们用大O标记法来表示的话,T(n)就等于 O(logn)。所以归并排序的时间复杂度是O(nlogn)。
从我们的原理分析和伪代码可以看出,归并排序的执行效率与要排序的原始数组的有序成都无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
-
归并排序的空间复杂度是多少?
归并排序的时间复杂度任何情况下都是 O(nlogn),看起来非常优秀。(待会儿你会发现,即便是快速排序,最坏情况下,时间复杂度也是O(n²))但是,归并排序并没有像快速排序那样,应用广泛。因为它有一个致命的弱点,那就是归并排序不是原地排序算法。
这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。
如果我们继续按照分析递归时间复杂度的方式,通过递推公式求解,那整个归并过程需要的空间复杂度就是O(nlogn)。
实际上,递归代码的空间复杂度并不能像时间复杂度那样累加。刚刚我们忘记了最重要的一点,那就是,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超狗n个数据的大小。所以空间复杂度是O(n)。
快速排序的原理
快速排序(Quicksort),我们习惯性简称为“快排”。快排可用的也是分治思想。乍看起来,它有点像归并排序,但是思路其实完全不一样。
快排的思想是这样的:如果要排序数组中下标从p到r的一组数据,我们选择p到r之间的任意一个数据作为 pivot(分区点)。
我们遍历p到r之间的数据,将小于 pivot 的放到左右,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组p到r之间的数据就被分成了三个部分,前面p打牌q-1之间都是小于 pivot 的,中间是 pivot,后面的q+1到r之间是大于 pivot的。
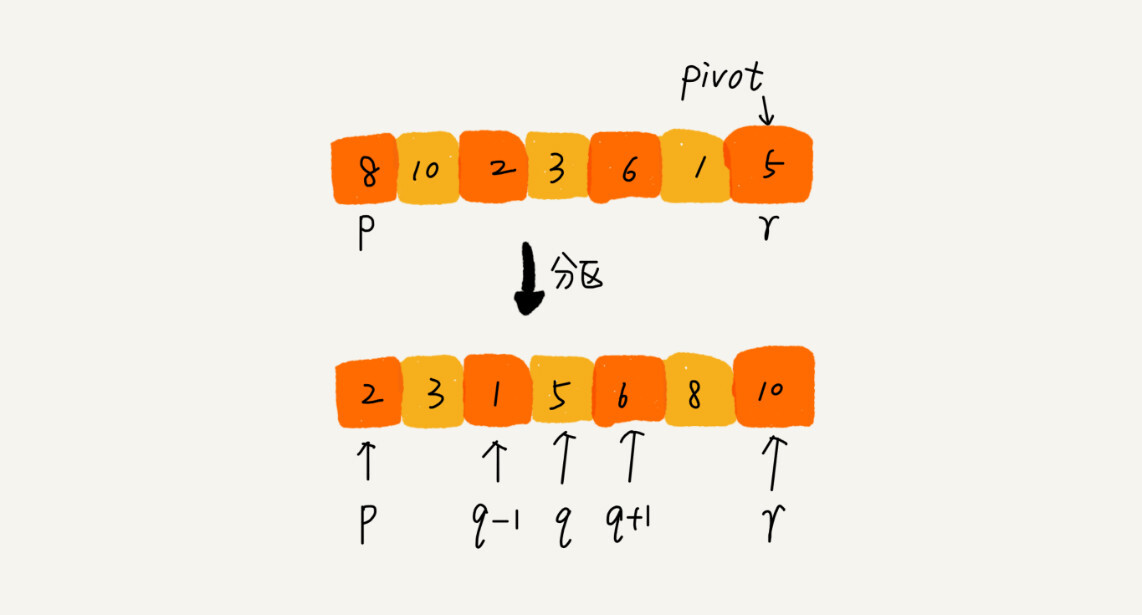
根据分治、递归的处理思想,我们可以用递归排序下标从p到q-1之间的数据和下标从q+1到r之间的数据,直到区间缩小为1,就说明所有的数据都有序了。
如果我们用递推公式来将上面的过程写出来的话,就是这样:
递推公式:
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)
终止条件:
p >= r下面是伪代码
// 快速排序,A是数组,n表示数组的大小
quick_sort(A, n) {
quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数,p,r为下标
quick_sort_c(A, p, r) {
if p >= r then return
q = partition(A, p, r) // 获取分区点
quick_sort_c(A, p, q-1)
quick_sort_c(A, q+1, r)
}递归排序中有一个 merge() 合并函数,我们这里有一个 partition() 分区函数。partition() 分区函数实际上我们已经讲过,就是随机选择一个元素作为 pivot(一般情况下,可以选择p到r区间的最后一个元素),然后对 A[p...r] 分区,函数返回 pivot 的下标。
如果我们不考虑空间消耗的话,partition() 分区函数可以写的非常简单。我们申请两个临时数组X和Y,遍历 A[p...r],将小于pivot 的元素都拷贝到临时数组X,将大于 pivot 的元素都拷贝到临时数组Y,最后再将数组X和数组Y中数据顺序拷贝到 A[p...r]。
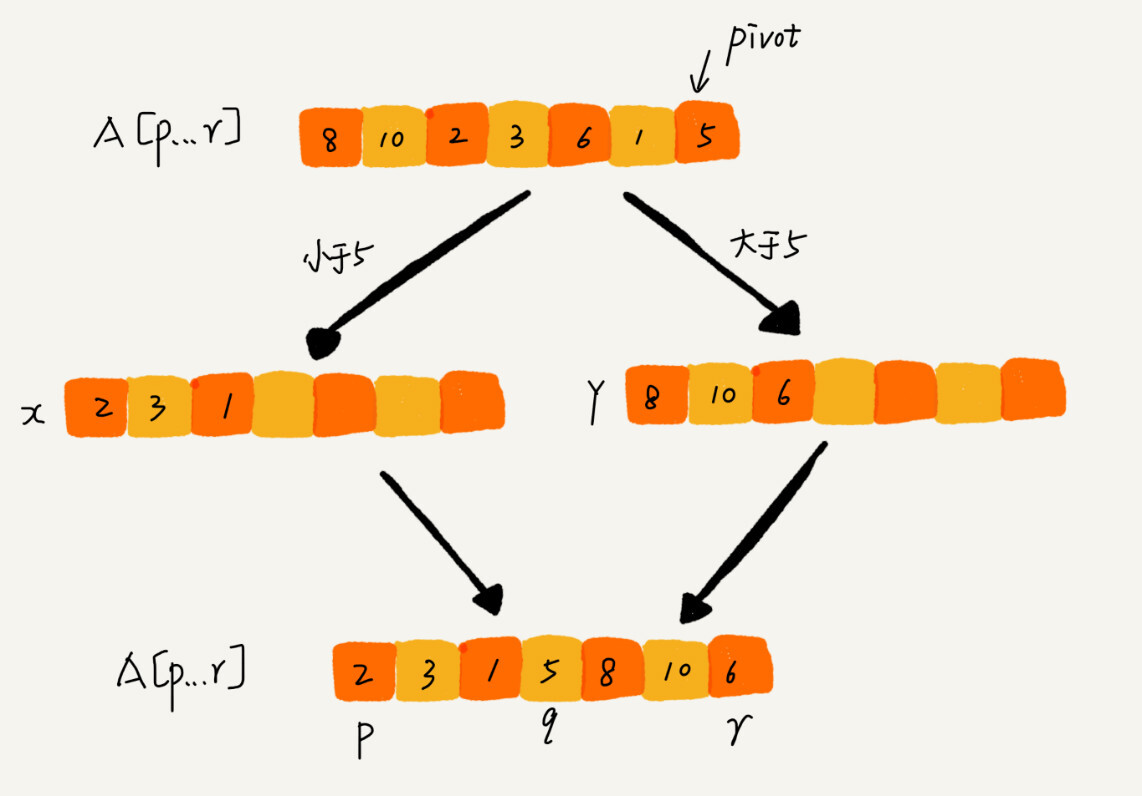
但是,如果按照这种思路实现的话,partition() 函数就需要很多额外的内存空间,所以快排就不是原地排序算法了。我们希望快排是原地排序算法,那他的空间复杂度得是O(1),那 partition() 分区函数就不能占用太多额外的内存空间,我们就需要在 A[p...r] 的原地完成分区操作
原地分区函数的实现思路非常巧妙。
partition(A, p, r) {
pivot := A[r]
i := p
for j := p to r-1 do {
if A[j] < pivot {
swap A[i] with A[j]
i := i+1
}
}
swap A[i] with A[r]
return i这里的处理有点类似选择排序。我们通过游标i把 A[p...r-1] 分成两部分。A[p...i-1] 的元素都是小于 pivot 的,我们暂且叫它“已处理区间”,A[i...r-1]是“未处理区间”。我们每次都从未处理的区间 A[i...r-1]中取出一个元素 A[j],与 pivot 对比,如果小于 pivot,则将其加入到已处理区间的尾部,也就是A[i]的位置。
数组的插入操作还记得吗?在数组某个位置插入元素,需要搬移数据,非常耗时。当时我们也讲了一种处理技巧,交换,在O(1)的时间复杂度内完成插入操作。这里我们也借助这个思想,只需要将A[i]与A[j]交换,就可以在O(1)时间复杂度内将A[j]放到下标为i的位置。
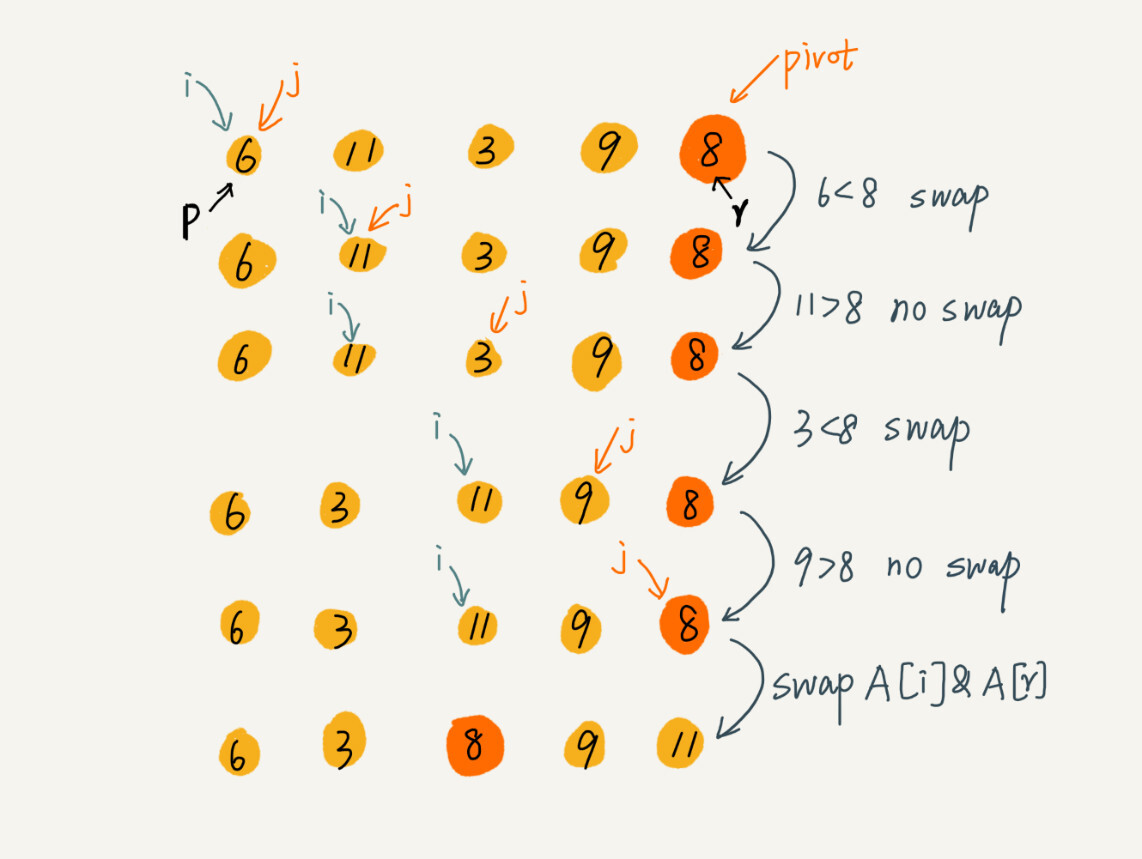
因为分区的过程涉及交换操作,如果数组中有两个相同的元素,比如序列6,8,7,6,3,5,9,4,在经过第一次分区操作之后,两个6的相对先后顺序就会改变。所以,快速排序并不是一个稳定的排序算法。
快速排序和归并排序用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢?
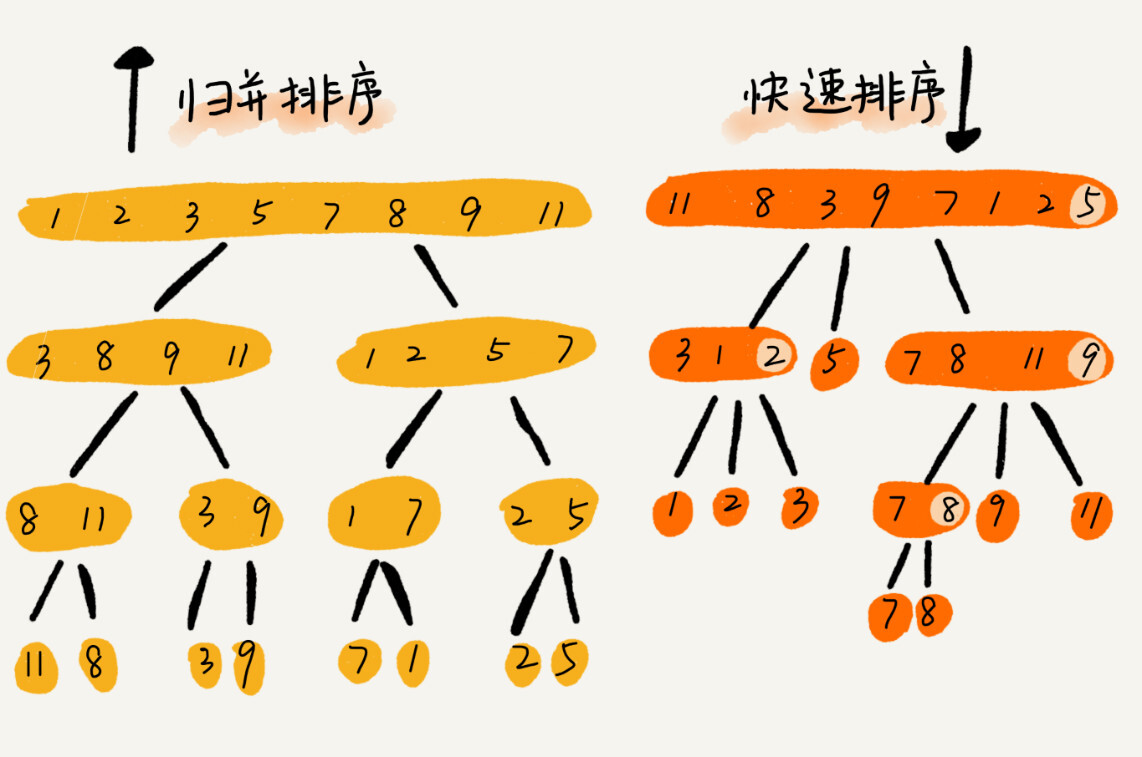
可以发现,归并排序的处理过程是由下到上,先处理子问题,然后再合并。而快速排序正好相反,它的过程是由上到下,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为O(nlogn)的排序算法,但是它是非原地排序算法。归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
快速排序的性能分析
快排也是用递归来实现的。对于递归代码的时间复杂度,前面总结的公式在这里也还是适用的。如果每次分区操作,都正好把数组分成大小接近想等的两个小区间,那快排的时间复杂度递推求解公式跟归并是相同的。所以,快排的时间复杂度也是O(nlogn)。
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。
T(n) = 2*T(n/2) + n; n>1但是,公式城里的前提是每次分区操作,我们选择的 pivot 都很合适,正好能将大区间对等的一分为二。但实际上这种情况是很难实现的。
如果数组中的数据原来已经是有序的了,比如1,3,5,6,8.如果我们每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约n次分区操作,才能完成快排的整个过程。每次分区我们都平均要扫描大学n/2个元素,这种情况下,快排的时间复杂度就从O(nlogn)退化成了O(n²)。
一个分区均匀一个分区不均匀,它们分别对应快排的最好情况时间复杂度和最坏情况时间复杂度。那平均情况时间复杂度呢?
假设每次分区操作都将分区分成大小为9:1的两个小区间。我们继续套用递归时间复杂度的递推公式:
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。
T(n) = T(n/10) + T(9*n/10) + n; n>1这个公式的递推求解的过程非常复杂,虽然可以求解,但不推荐。实际上,递归的时间复杂度的求解方法除了递推公式之外,还有递归树。
如何用快排思想在O(n)内查找第K大元素
快速排序的核心思想就是分治和分区,我们可以利用分区的思想,来解答这个问题。
我们选择数组区间 A[0...n-1]的最后一个元素 A[n-1] 作为 pivot,对数组 A[0...n-1] 原地分区,这样数组就分成了三个部分,A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K,那 A[p] 就是求解的元素;如果 K>p+1,说明第K大元素出现在 A[p+1...n-1] 区间,我们再按照上面的思路递归的在 A[p+1...n-1] 这个区间内查找。同理,如果 K<p+1,那我们就在 A[0...p-1] 区间查找。