数据挖掘三：相关分析

前言

哲学告诉我们世界是一个普遍联系的有机整体，现象之间客观上存在着某种有机联系。一种现象的发展变化，必然受与之相关联的其他现象发展变化的制约与影响，在统计学中这种依存关系可以分成相关关系回归函数关系两大类。

研究意义

1. 相关系数(correlation coefficient)

   相关系数是变量间关系程度的最基本测度之一

2. 相关分析(correlation analysis)

   是研究现象之间是否存在某种依存关系，并对具体有依存关系的现象探讨其相关方向以及相关程度，是研究随机变量之间的相关关系的一种统计方法

相关系数的基本特征

1. 方向(direction)
   1. 正相关(positive correlation)：两个变量变化方向相同
   2. 负相关(negative correlation)：两个变量变化方向相反
2. 量级(magnitude)
   1. 低度相关：0≤|r|＜0.3
   2. 中度相关：0.3≤|r|＜0.8
   3. 高度相关：0.8≤|r|＜1

计算公式

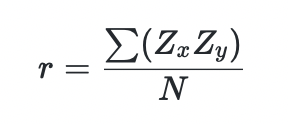
r : 相关系数
Zx: 变量X的z分数
Zy: 变量Y的z分数
N : X和Y取值的配对个数

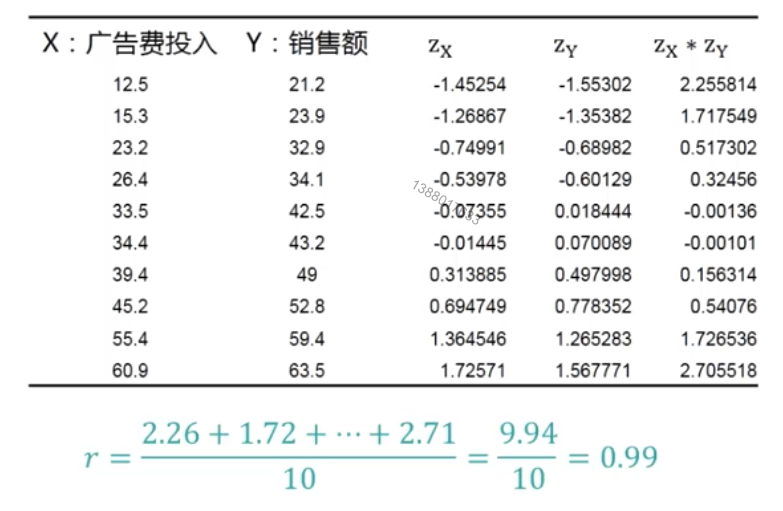
计算公式案例

z分数计算：每个变量中的值减去该变量的均值除以标准差

代码

import numpy

X = [
    12.5, 15.3, 23.2, 26.4, 33.5,
    34.3, 39.4, 45.2, 55.4, 60.9
]

Y = [
    21.2, 23.9, 32.9, 34.1, 42.5,
    43.2, 49.0, 52.8, 59.4, 64.5
]

# 均值
# mean函数求均值，
# 参数axis=0计算多维数组每一列的均值
# 参数axis=1计算多维数组每一行的均值
XMean = numpy.mean(X)
YMean = numpy.mean(Y)

# 标准差
# 标准差 = 每个数减去平均数的平方相加除以个数，再开平方
# 参数axis=0计算多维数组每一列的标准差
# 参数axis=1计算多维数组每一行的标准差
XSD = numpy.std(X)
YSD = numpy.std(Y)

# z分数
# z分数 = (每个变量的值 - 均值) / 标准差
ZX = (X - XMean) / XSD
ZY = (Y - YMean) / YSD

# 相关系数手动计算
r = numpy.sum(ZX * ZY) / (len(X))

# 相关系数numpy计算
r = numpy.corrcoef(X, Y)

# 相关系数pandas计算
import pandas
data = pandas.DataFrame({
    'X': X,
    'Y': Y
})
r = data.corr()

相关系数是理解两个变量是否相关的指标，但是不能过分依赖，搜索“安斯库姆四重奏”得到答案

numpy和pandas计算出来的相关系数r为矩阵，对角线都为1，所以为对称矩阵，暂不清楚意义，整明白了补充