如何选择合适的排序算法?
如果要实现一个通用的、高效率的排序函数,应该选择哪种排序算法?
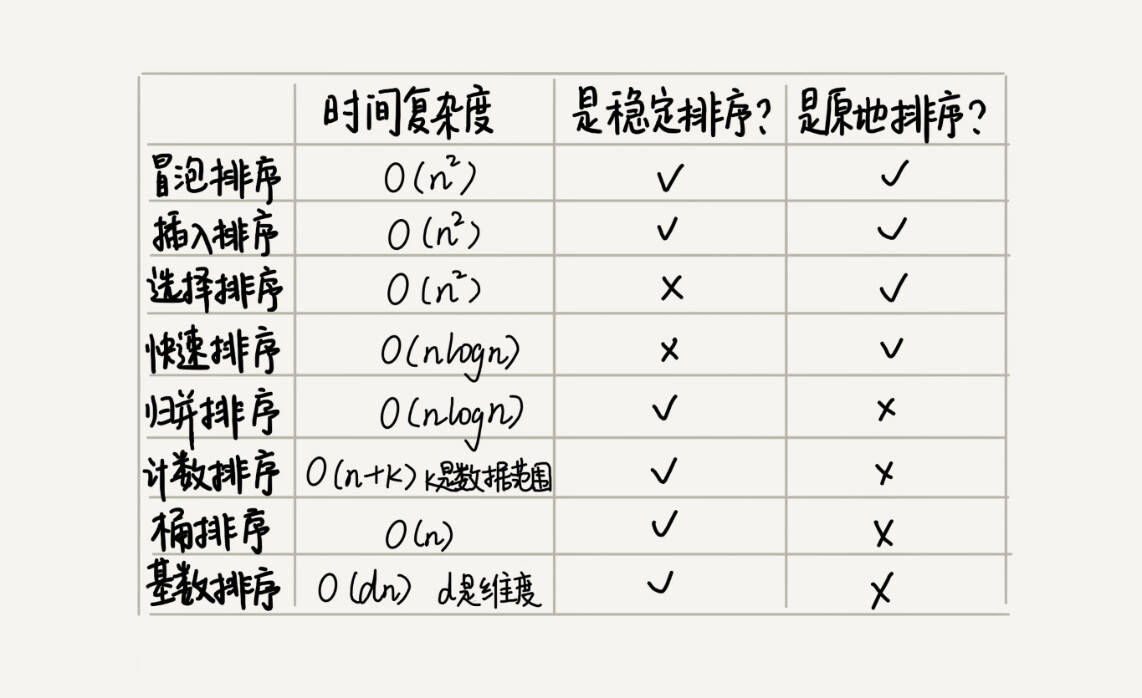
前面讲过,线性排序算法的时间复杂度比较低,适用场景比较特殊。所以如果要写一个通用的排序函数,不能选择线性排序算法。
如果对小规模数据进行排序,可以选择时间复杂度是 O(n2) 的算法;如果对大规模数据进行排序,时间复杂度是 O(nlogn) 的算法更加高效。所以,为了兼顾任意规模数据的排序,一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
时间复杂度是 O(nlogn) 的排序算法不止一个,我们已经讲过的有归并排序、快速排序,后面讲堆的时候我们还会讲到堆排序。堆排序和快速排序都有比较多的应用,比如 Java 语言采用堆排序实现排序函数,C 语言使用快速排序实现排序函数。
不知道你有没有发现,使用归并排序的情况其实并不多。我们知道,快排在最坏情况下的时间复杂度是 O(n2),而归并排序可以做到平均情况、最坏情况下的时间复杂度都是 O(nlogn),从这点上看起来很诱人,那为什么它还是没能得到“宠信”呢?
因为归并排序并不是原地排序算法,空间复杂度是 O(n)。所以,粗略点、夸张点讲,如果要排序 100MB 的数据,除了数据本身占用的内存之外,排序算法还要额外再占用 100MB 的内存空间,空间耗费就翻倍了。
快速排序比较适合来实现排序函数,但是,快速排序在最坏情况下的时间复杂度是 O(n2),如何来解决这个“复杂度恶化”的问题呢?
如何优化快速排序?
为什么最坏情况下快速排序的时间复杂度是 O(n2) 呢?如果数据原来就是有序的或者接近有序的,每次分区点都选择最后一个数据,那快速排序算法就会变得非常糟糕,时间复杂度就会退化为 O(n2)。实际上,这种 O(n2) 时间复杂度出现的主要原因还是因为分区点选的不够合理。
那什么样的分区点是好的分区点呢?或者说如何来选择分区点呢?
最理想的分区点是:被分区点分开的两个分区中,数据的数量差不多。
如果很粗暴地直接选择第一个或者最后一个数据作为分区点,不考虑数据的特点,肯定会出现之前讲的那样,在某些情况下,排序的最坏情况时间复杂度是 O(n2)。为了提高排序算法的性能,我们也要尽可能地让每次分区都比较平均。
这里介绍两个比较常用、比较简单的分区算法。
-
三数取中法
我们从区间的首、尾、中间,分别取出一个数,然后对比大小,取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度,取数据出来比较,将中间值作为分区点的分区算法,肯定要比单纯取某一个数据更好。但是,如果要排序的数组比较大,那“三数取中”可能就不够了,可能要“五数取中”或者“十数取中”。
-
随机法
随机法就是每次从要排序的区间中,随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好,但是从概率的角度来看,也不大可能会出现每次分区点都选的很差的情况,所以平均情况下,这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况,出现的可能性不大
我们知道,快速排序是用递归来实现的。在递归那一节讲过,递归要警惕堆栈溢出。为了避免快速排序里,递归过深而堆栈过小,导致堆栈溢出,有两种解决办法:第一种是限制递归深度。一旦递归过深,超过了我们事先设定的阈值,就停止递归。第二种是通过在堆上模拟实现一个函数调用栈,手动模拟递归压栈、出栈的过程,这样就没有了系统栈大小的限制。
举例分析排序函数
为了让你对如何实现一个排序函数有一个更直观的感受,我拿 Glibc 中的 qsort() 函数举例说明一下。虽说 qsort() 从名字上看,很像是基于快速排序算法实现的,实际上它并不仅仅用了快排这一种算法。
如果你去看源码,你就会发现,qsort() 会优先使用归并排序来排序输入数据,因为归并排序的空间复杂度是 O(n),所以对于小数据量的排序,比如 1KB、2KB 等,归并排序额外需要 1KB、2KB 的内存空间,这个问题不大。现在计算机的内存都挺大的,我们很多时候追求的是速度。还记得我们前面讲过的用空间换时间的技巧吗?这就是一个典型的应用。
但如果数据量太大,就跟我们前面提到的,排序 100MB 的数据,这个时候我们再用归并排序就不合适了。所以,要排序的数据量比较大的时候,qsort() 会改为用快速排序算法来排序。
那 qsort() 是如何选择快速排序算法的分区点的呢?如果去看源码,你就会发现,qsort() 选择分区点的方法就是“三数取中法”。是不是也并不复杂?
还有递归太深会导致堆栈溢出的问题,qsort() 是通过自己实现一个堆上的栈,手动模拟递归来解决的。
实际上,qsort() 并不仅仅用到了归并排序和快速排序,它还用到了插入排序。在快速排序的过程中,当要排序的区间中,元素的个数小于等于 4 时,qsort() 就退化为插入排序,不再继续用递归来做快速排序,因为我们前面也讲过,在小规模数据面前,O(n2) 时间复杂度的算法并不一定比 O(nlogn) 的算法执行时间长。我们现在就来分析下这个说法。
时间复杂度代表的是一个增长趋势,如果画成增长曲线图,你会发现 O(n2) 比 O(nlogn) 要陡峭,也就是说增长趋势要更猛一些。但是,我们前面讲过,在大 O 复杂度表示法中,我们会省略低阶、系数和常数,也就是说,O(nlogn) 在没有省略低阶、系数、常数之前可能是 O(knlogn + c),而且 k 和 c 有可能还是一个比较大的数。
假设 k=1000,c=200,当我们对小规模数据(比如 n=100)排序时,n2的值实际上比 knlogn+c 还要小。
knlogn+c = 1000 * 100 * log100 + 200 远大于10000
n^2 = 100*100 = 10000所以,对于小规模数据的排序,O(n2) 的排序算法并不一定比 O(nlogn) 排序算法执行的时间长。对于小数据量的排序,可以选择比较简单、不需要递归的插入排序算法。
还记得哨兵来简化代码,提高执行效率吗?在 qsort() 插入排序的算法实现中,也利用了这种编程技巧。虽然哨兵可能只是少做一次判断,但是毕竟排序函数是非常常用、非常基础的函数,性能的优化要做到极致。



